¿Qué es la secuencia numérica Fibonacci?

La secuencia de Fibonacci es una de las más conocidas y estudiadas en el mundo de las matemáticas. Esta serie numérica, compuesta por números enteros positivos, ha sido utilizada durante siglos por matemáticos, artistas, músicos y científicos de todo tipo. Pero ¿qué es exactamente la secuencia de Fibonacci y cómo se relaciona con el mundo que nos rodea? En este artículo exploraremos la historia y los usos de esta fascinante secuencia numérica, y descubriremos cómo se encuentra presente en la naturaleza, en el arte y en la cultura popular.

El origen de la secuencia numérica Fibonacci

Leonardo de Pisa, más conocido por su apodo Fibonacci, una abreviación de filius Bonacci —hijo de Bonacci— fue un matemático italiano que introdujo la secuencia en Europa en su libro “Liber Abaci”, publicado en 1202. El libro trataba sobre el cálculo indo-árabe y cómo podía ser utilizado en el mundo occidental. La secuencia de Fibonacci se presentaba en el libro como un problema de reproducción de conejos, pero rápidamente se convirtió en un objeto de estudio matemático en sí mismo.

Fibonacci había estudiado matemáticas en el norte de África (en el territorio de la actual Algeria) y había aprendido sobre el cálculo indo-árabe durante su viaje. Luego de estudiar en África, viajó por los territorios de las hoy Grecia, Egipto y Siria, teniendo la oportunidad de estudiar distintos sistemas numéricos y operaciones aritméticas. Al traer estos conocimientos a Europa, contribuyó significativamente a la introducción del sistema de base 10 (que utilizamos hoy en día) en el mundo occidental. La secuencia de Fibonacci también se convirtió en una parte importante de su legado matemático. Aunque no es el primer matemático en haber descubierto la secuencia (la cual apareció en sánscrito escrita por el poeta y matemático indio Pingala aproximadamente en el siglo 2 A.C.), Fibonacci es conocido por haberla popularizado y dado a conocer en Europa.

¿Quién fue Leonardo Fibonacci?

Leonardo Bigollo, como solía firmar ocasionalmente, vivia en la frenética ciudad de Pisa, puerto clave en el intercambio comercial del Mar Mediterráneo. Allí, Leonardo probablemente observó a los mercaderes italianos realizar cuentas diariamente con números romanos, y utilizar el ábaco para realizar operaciones simples. En la ciudad de Pisa se había desarrollado una importante industria del cuero, además de todos los productos característicos del norte y centro de Italia. Realizar operaciones con números romanos era realmente poco práctico. Para sumar 3786 y 3843, era necesario agregar MMMDCCLXXXVI a MMMDCCCXLIII. Ni hablar de realizar operaciones de multiplicación.

En la ciudad de Bugia, en Algeria, Leonardo conoció el sistema Indio de 9 figuras, probablemente gracias a algún instructor árabe. Al comparar los distintos sistemas numéricos, decidió publicar un libro para fomentar el uso del sistema numérico Indo-árabe a Europa. En su libro, Leonardo presenta numerosos ejemplos sobre cómo convertir los números romanos al nuevo sistema, y su utilización en operaciones matemáticas. Su libro incluía un ejemplo sobre cómo utilizar esta secuencia numérica en la reproducción de conejos. Su ejemplo fue retomado más adelante, entre los siglos 17 y 19, por varios matemáticos, y es por ello que reconocemos a Leonardo de Pisa, o Leonardo Fibonacci, como el divulgador principal de la sucesión que hoy lleva su nombre. Para descubrir la historia de este fascinante número, recomiendo la lectura del libro «La razón áurea: la historia de phi, el número más sorprendente del mundo», en inglés en el link provisto.

Uno de los principales responsables de que llamemos a esta secuencia «Fibonacci» fue el matemático francés del siglo 19, Édouard Lucas (1842-1891).

La secuencia numérica Fibonacci en la naturaleza

El número áureo se encuentra repetidamente en la naturaleza como una guía de crecimiento que permite el esfuerzo más eficiente en el proceso de desarrollo de numerosas especies de plantas. Las hojas incipientes alrededor de un tallo, las semillas de la flor del girasol, las piñas de las coníferas son todos ejemplos de cómo la naturaleza encontró en la matemática una forma de desarrollo armonioso y perfecto.

Los números que componen la secuencia numérica de Fibonacci, y su relación con el número áureo

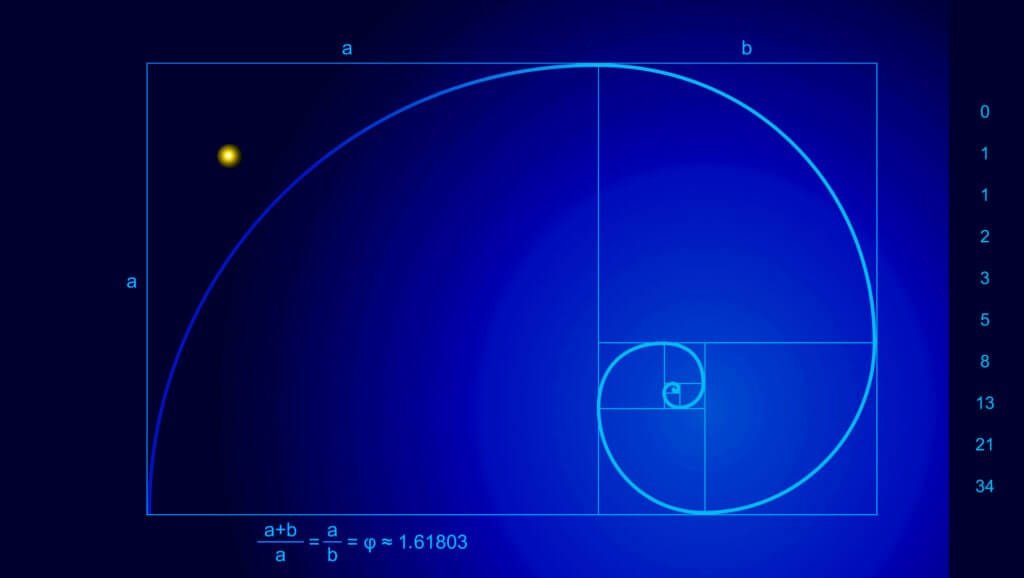
La secuencia de Fibonacci comienza con los números 0 y 1, y cada número siguiente se calcula sumando los dos anteriores. Por lo tanto, la secuencia se presenta de la siguiente manera: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, y así sucesivamente. Aunque esta secuencia puede parecer simple en un primer momento, se ha demostrado que tiene una serie de propiedades matemáticas y aplicaciones sorprendentes.

Una de las características más notables de la secuencia de Fibonacci es que cada número es aproximadamente 1.618 veces mayor que el anterior, lo que se conoce como el “número áureo” o “proporción áurea”. Esta proporción se encuentra en una gran variedad de contextos, desde la arquitectura y el arte hasta la biología y la psicología. Por ejemplo, la proporción áurea se encuentra en la disposición de las hojas en las ramas de muchas plantas, en la forma en que las conchas de mar se expanden y en la estructura del ADN. También se ha demostrado que esta proporción es atractiva visualmente para los seres humanos, y por lo tanto se utiliza a menudo en el diseño gráfico y la publicidad.

Además de su relación con la proporción áurea, la secuencia de Fibonacci también tiene una serie de otras aplicaciones matemáticas y algorítmicas. Por ejemplo, se ha utilizado para resolver problemas de optimización y para generar números aleatorios. Está relacionada con otras series numéricas importantes, como la secuencia de Lucas y la secuencia de Pell.

La secuencia de Fibonacci es una serie numérica sorprendentemente versátil y fascinante, que ha sido utilizada y estudiada durante siglos.

¿Puede aplicarse la secuencia numérica Fibonacci para el desarrollo económico?

Si bien es cierto que la secuencia de Fibonacci ha sido utilizada principalmente en el ámbito matemático y científico, es interesante explorar su posible aplicación en otras áreas, como el desarrollo económico.

Si consideramos que la secuencia de Fibonacci favorece el desarrollo natural de ciertas especies en la naturaleza, quizás sea posible aplicar sus propiedades para favorecer el desarrollo económico de las personas y luchar contra la pobreza. Tal vez exista una forma de utilizar la secuencia de Fibonacci para crear un sistema económico más justo y equilibrado.

Por ejemplo, podría imaginar un sistema impositivo basado en la secuencia de Fibonacci, en el que las tasas impositivas aumentaran de manera gradual. Esto podría generar un escenario propicio para el desarrollo económico de los individuos y las empresas, ya que habría un incentivo para generar riqueza de manera sostenible y equilibrada.

La cuestión impositiva divide actualmente de forma tajante a la población. Para algunos, los impuestos son la forma de redistribuir un ingreso exagerado, mientras que otros favorecen una carga impositiva baja que estimule la generación de empleo para impulsar el desarrollo.

Paradójicamente, las víctimas de esta disputa ideológica son los pequeños contribuyentes. Las pequeñas y medianas empresas generalmente ven restringida su capacidad de crecimiento a causa de la carga impositiva que recae sobre ellas, especialmente cuando no tienen un régimen impositivo diferenciado de las grandes empresas. ¿Existe acaso, alguna fórmula precisa para el desarrollo?

Fibonacci aplicado al desarrollo de los individuos y la economía

Gracias a sus propiedades matemáticas, una de sus mayores virtudes de la secuencia numérica Fibonacci es la flexibilidad: se puede asignar un incremento de un punto porcentual a cada salto en la secuencia, o dos puntos porcentuales, o cinco, etc. Además, se puede establecer el tope máximo de acuerdo a la política preferida por el gobierno (20%, 24%, 30%), y realizar un corte anticipado de la tasa máxima en los sectores económicos que se busque favorecer (por ejemplo, un tope máximo del 12% para la exportación de servicios basados en el conocimiento).

De este modo, se pueden adoptar dos o tres secuencias diferenciadas, una para empresas, otra para asalariados y otra para autónomos. Por ejemplo:

• Las utilidades de las empresas pueden ser gravadas con una escala que progrese de a dos puntos porcentuales, dando la libertad suficiente al desarrollo de las PyMEs. Atribuyendo números de forma arbitraria que deberían ser ajustados a la moneda local de cada país, una posible equivalencia podría ser la siguiente :
  • Ganancia anual hasta $118 mil, tributaría 2%
  • Ganancia anual hasta $178 mil, tributaría 4%
  • Ganancia anual hasta $297 mil, tributaría 6%
  • Ganancia anual hasta $475 mil, tributaría 8%
  • Ganancia anual hasta $773 mil, tributaría 10%
  • Ganancia anual hasta $1,248 millón, tributaría 12%
  • Ganancia anual hasta $2,022 millones, tributaría 14%
  • Ganancia anual hasta $3,270 millones, tributaría 16%
  • Ganancia anual hasta $5,292 millones, tributaría 18%
  • Ganancia anual hasta $8,562 millones, tributaría 20%
  • Ganancia anual hasta $13,854 millones, tributaría 22%
  • Ganancia anual hasta $22,416 millones, tributaría 24%
  • Toda ganancia anual superior tributaría el 26%

• Un trabajador asalariado cuyo mínimo no imponible para el pago de Impuesto a las Ganancias ronda los 50 mil pesos mensuales, con una escala que progrese de acuerdo a la secuencia en cuestión :
  • Salario bruto anual desde $601 mil, tributaría 5%
  • Salario bruto anual desde $773 mil, tributaría 8% o 13%
  • Salario bruto anual desde $1,546 millones, tributaría 21%
  • Salario bruto anual desde $2,319 millones, tributaría 34%

Del mismo modo, para los autónomos se puede armar una escala similar a la aplicada para las empresas, pero aplicando la alícuota a una quinta parte del monto más arriba mencionado:

• Un autónomo que obtenga:
  • Ingreso anual de $23,8 mil, tributaría 2%
  • Ingreso anual de $35,7 mil, tributaría 4%
  • Ingreso anual de $59,5 mil, tributaría 6%
  • Ingreso anual de $95,1 mil, tributaría 8%
  • Ingreso anual de $154,6 mil, tributaría 10%
  • Ingreso anual de $249,8 mil, tributaría 12%
  • Ingreso anual de $404,3 mil, tributaría 14%
  • Ingreso anual de $654,0 mil, tributaría 16%
  • Ingreso anual de $1.058,4 millón, tributaría 18%
  • Ingreso anual de $1.712,5 millón, tributaría 20%
  • Ingreso anual de $2.770,8 millones, tributaría 22%
  • Ingreso anual de $4.483,3 millones, tributaría 24%
  • Todo ingreso anual superior a $7.254 millones tributaría el 26%

Una nota especial para contextos inflacionarios

Todo sistema impositivo requiere establecer una nominalidad. En un país con un contexto inflacionario como el argentino, por ejemplo, equivocar la nominalidad genera un conflicto social, ya que el constante aumento en el nivel de precios empuja un aumento salarial ficticio que contrasta con un sistema impositivo anclado en moneda local. En consecuencia, el resultado final es un salario decreciente año tras año para el trabajador por la mayor porción de impuestos que se le descuentan de sus haberes. Al mismo tiempo, las PyMEs atraviesan los vaivenes económicos con incertidumbre sobre la situación económica futura pero con la certeza de que el Estado cobrará un porcentaje fijo sobre una ganancia que, a precios constantes, probablemente exceda el concepto de «ganancia».

Para evitar esta situación se puede recurrir a distintas alternativas, como pueden ser por ejemplo las «Unidades de Valor Adquisitivo» (UVAs). Una vez definida la unidad de medida sobre la cual establecer una nominalidad, se puede aplicar a la misma un crecimiento paulatino que en nuestro caso está dado por los valores de la secuencia Fibonacci.